

#Abcd matrix series
The ABCD parameters of a series impedance are given by: For instance, the equivalent T model derived from the ABCD parameters of an amplifier IC can be examined to determine the bond wire inductance, which can be tuned out with a judicious selection of coupling capacitor.įor reference, the ABCD parameters of a shunt admittance Y are given by: Finding this relationship drives the choice of a π or T network.

Applying this concept to an unknown component, the ABCD parameters can be examined to see if the reactance of the first series element of the T network or the admittance of the first shunt element of the π network is directly proportional to f or 1/f. With a little mathematics, it was straightforward to derive a π network model of this inductor. The actual value of Z is:ĭividing the imaginary part by 2 π*200 MHz gives 12.4 nH, which is close to the expected inductance of 12.5 nH.įigure 6 Adding the inter-winding capacitance to the π model for the inductor. One might expect symmetry, yet with more digits of accuracy, S 11 is not precisely equal to S 22, and S 21 is not precisely equal to S 12. The inductor’s S-parameters at 200 MHz, available from Coilcraft’s website, are:Ĭonverting the S-parameters to the ABCD (T) parameters: Using parameter extraction, we would like to know the equivalent circuit for the inductor, including its parasitics. For RF applications, the Spring series are high Q inductors, although the footprint may be too large for some designs. To apply the concept, consider a 12.5 nH air core inductor, such as the Coilcraft A04T MiniSpring. The conversion from 50 Ω S-parameters to the equivalent ABCD matrix is given by: For a two-port network, the ABCD parameters are defined as 1:įor the T network, the ABCD parameters are:Īgain, the Y term is obvious, and the Z terms are easily derived. ABCD parameters, which are also known as cascade, chain or T parameters, are particularly useful for this purpose. While this simple example assumes ideal components, it is reasonable to say that stray capacitance between the nodes of a lowpass filter is detrimental - which is why high isolation, lumped-element lowpass filters have shields between sections, where the capacitors to ground are implemented with a feedthrough capacitor in the wall of each shield.Īctual components are never ideal, making mathematical extraction useful to understand their limitations. Above 4 GHz, the isolation is clearly compromised by the stray capacitance. Figure 1 plots the response of a three element, 500 MHz Butterworth filter, showing the effect of 0.1 pF stray capacitance across an ideal inductor. To illustrate, knowing that a 0.1 pF effective capacitance exists between the nodes of a lowpass filter might lead to a superior design: shielding between the nodes, resulting in greater stopband isolation. To aid this understanding, RLC parameter extraction can be very enlightening. The intuitive understanding of an RF network is only possible if its behavior can at least be understood in first order terms. What is particularly noteworthy about the angle of the ray after the transformation?Īnd the answering of these questions should show you how the transfer matrix encodes the lens's collimating behavior for all points on the focal plane.Figure 1 |S 21| response of a 500 MHz Butterworth lowpass filter, showing the effect of a 0.1 pF stray capacitance in parallel with the ideal inductor.So your task is to work out what the transfer matrix in (1) does to this state, i.e. Before we begin, I believe your transfer matrix should be:
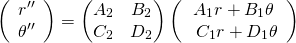
In fact, you compute the image given the object position by using the unique, fixed transfer matrix characterizing an optical element. So it doesn't depend at all on where the object and image are. As such, it is meant to work for all cases, at least approximately, over a range of inputs. A transfer matrix is a representation of a homogeneous linear function that approximates a behavior.


 0 kommentar(er)
0 kommentar(er)
